Si por un acto de magia alguien hiciera que pi se escribiera a sí mismo, el resultado sería un caos.
Si por un acto de magia alguien hiciera que pi se escribiera a sí mismo, el resultado sería un caos.
Imagínate que comenzara a sustituir todas las letras de este libro por sus propias cifras: ... 653589793238462643383279 … Acabaría con todas las letras para continuar escribiéndose, 0836510925381… llenaría los márgenes en blanco y saltaría a un libro próximo. Allí, borraría todos los caracteres y seguiría 4873562005432123776543…
Cuando hubiese acabado con todos los libros de la casa, continuaría por los periódicos y las revistas: 331234560121223… Cubriría el dorso de las fotos, los billetes de banco y las sábanas y almohadas de la cama: 8810987652901…Llenaría la ropa, las paredes, los rollos de papel higiénico y, cuando todo estuviera lleno de números, pasaría a la casa vecina y haría lo mismo.
Emborronaría todos los sitios posibles del lugar en que vives, incluyendo las guías telefónicas y los libros de todas las bibliotecas… No quedarían una letra ni un número sanos.
Pero la cosa no habría hecho más que comenzar, porque de un pueblo saltaría a otro, desenrollándose por las carreteras y los caminos (sin olvidar los coches ni las motos) como algo contagioso y seguiría escribiéndose: 11349982781…
No quedaría un lugar de la Tierra libre de las cifras de pi: ni las hojas de los árboles, ni el dorso de las hormigas, ni los granos de arena… y acabado el trabajo en el planeta, viajaría por el espacio y seguiría escribiéndolo en la Luna… Y cuando la Luna estuviese escrita…
Terrorífico. Mejor no saber de magia.
En 1983, un memorión llamado Rajan Mahdevan recitó de memoria más de treinta mil cifras decimales de pi. Más o menos, eso llenaría unas dieciocho páginas de este libro. ¿Para qué sirve esto? Para nada, evidentemente. ¿Para qué sirven todas esas cifras de pi? Pues para nada, tampoco; pero pi es así.
Hay números que son tan complicados como pi, puestos a desenrollarse. Por ejemplo, 1/3 lo llenaría todo de treses: 0,33333 … La fracción 1/7 lo llenaría todo con 142857. Como sabemos, a estas cifras que se repiten de forma ilimitada se las llama periódicas. Pi se diferencia de 113 y de 1/7 en que sus cifras no son periódicas; es decir, no se repiten nunca.
Otros muchos números son no periódicos, como por ejemplo: 0,12345678910111213… (hay infinitos de la misma clase, que tú puedes construir) pero estos son previsibles. Por ejemplo, después de 8756 8757 875… sigue un ocho. En el caso de pi, no se sabe qué número sigue, a no ser que se calcule (lo cual, a partir de un cierto límite, tiene su dificultad).
Conozcamos mejor el número pi
¿Diremos por eso que pi es un número «raro»? Sí y no. También √2 tiene un número infinito de cifras imprevisibles, pero hay una diferencia importante entre pi y √2. Mientras este es una solución de la ecuación “el cuadrado de un número es igual a 2”, pi no es una solución de ninguna ecuación de coeficientes racionales. A pi (y a una gran familia de números) se les llama números trascendentes. ¡Toma ya! Pero no vamos a liarnos por este camino.
Antes de nada, vamos a variar la forma de escribirlo. Todo el mundo lo conoce con la legra griega π, que se lee «pi», y es famoso por aparecer en fórmulas como L = 2.π.r y S = π.r2, entre otras muchas. Pese a todo, no fueron los griegos quienes le dieron ese nombre. Los griegos no tenían cifras para escribir cantidades, y utilizaban letras. Paras ellos, π’ (pi con acento) representaba 80, mientras, ‘π (apóstrofo pi) representaba 80000. Nunca pensaron que algún día expresaría el cociente entre la longitud de una circunferencia y la de su diámetro, que es lo que expresa actualmente.
Un poco de historia
La primera persona que utilizó la letra π con este propósito fue un tal Jones, en 1706, pero nadie le hizo mucho caso, hasta que el mejor matemático de la época, Euler, en 1737, lo empleó en sus cálculos. Entonces, todo el mundo dijo: «Ah, si lo hace Euler … ». Y todo el mundo lo aceptó.
Hoy sabemos que π vale, aproximadamente, 3,141592. Pero, desde hace siglos, los constructores e ingenieros de todas las épocas han tratado de acercarse al valor más preciso posible. Cuando las obras eran toscas, bastaba con saber que la circunferencia era tres veces mayor que el diámetro. Eso era suficiente porque, después de todo, los círculos nunca salían muy redondos. Pero cuando se ganó en precisión y había que calcular, por ejemplo, el diámetro del agujero en que debía encajar una columna, se dijo: «tres y un poco más». La mejor aproximación de los primeros tiempos griegos era la fracción 22/7, que da un valor igual a 3,1428 … ¡No estaba nada mal!
Pero los ingenieros y los matemáticos, a veces, han sido un poco chinches. Arquímedes de Siracusa (287-212 a. de C.), que era un tipo muy brillante, se puso a calcular y llegó a la conclusión de que debía ser un poco más pequeño que 22/7 y un poco mayor que 223/71. Es decir, estaba comprendido entre 3,1428 y 3,1408. Si se tomara el valor promedio, se obtendría 3,1418, solo dos diezmilésimas por encima del valor más aproximado que utilizamos hoy.
Los matemáticos de entonces no utilizaban los números decimales como hoy lo hacemos. Se empleaban fracciones. Durante mucho tiempo, buscaron fracciones mejores que las de Arquímedes, pero no las encontraron… en Europa. Porque en el siglo V, un chino llamado Tsu Chung encontró la fracción 355/113, que da el valor π = 3,141592. ¡Seis cifras de precisión! Hay que tener presente que los chinos eran muy buenos matemáticos; ocho siglos antes de nuestra era, representaban π con la bonita fracción 92/29, que da como resultado 3,1724…
Hemos visto que el valor real de π es 3,141592653589… ¿Merece la pena seguir buscando más decimales? Comprobémoslo. Imaginemos que conocemos el valor exacto del radio de la Tierra (suponiendo que sea una esfera, que no lo es) y quisiéramos calcular la longitud del perímetro del ecuador, si fuera un círculo (que tampoco lo es). La diferencia entre utilizar la fracción de Tsu Chung y un valor de πcon veinte decimales daría un error de unos tres metros. Tres metros en casi cuarenta y un millones de metros no está nada mal, teniendo en cuenta que nuestro planeta no es perfecto, ni mucho menos.
Según parece, el matemático Al Kashi, en el observatorio de Sarnarcanda, obtuvo en el siglo XV el valor de π con una precisión de ¡catorce decimales! Pero eso, los científicos europeos no lo supieron hasta mucho más tarde. Estaban empeñados en buscar una fracción que diera el valor de π de una forma exacta, y a ello dedicaron muchas horas de sueño.
Los matemáticos pueden ser tercos, pero también ingeniosos. Hasta cierta época, la única manera de trabajar con figuras geométricas era dibujándolas. Pero algunos investigadores del siglo XVI descubrieron que había algo mejor: utilizar el álgebra. (En realidad, esto lo habían descubierto los matemáticos árabes, pero fue desarrollado por los europeos). Dijeron algo así como: «Arquímedes trabajó con polígonos que tenían cada vez más lados, acercándose a la forma de la circunferencia. Hagamos nosotros lo mismo, pero utilizando ecuaciones».
Vieta, en el siglo XVI
Atención, porque dentro de poco aparecerá un «monstruo» matemático, pero no hay que calcular sobre él. Los matemáticos dedujeron un procedimiento para trabajar con polígonos con tantos lados como quisieran, aplicando fórmulas. Por ejemplo, Vieta descubrió que para obtener el valor de π utilizando un polígono de 1024 lados (que no es una circunferencia, pero se le aproxima bastante) hay que calcular el valor de:
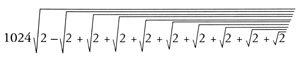
Trabajar con raíces cuadradas no era un plato agradable, sobre todo teniendo en cuenta que entonces no había calculadoras, pero los matemáticos tuvieron la esperanza de que, con paciencia, podrían aproximarse a π tanto como quisieran, ya que no encontraban una fracción mejor que 355/113. Trabajando con «monstruos» como el anterior, Vieta, en 1593, llegó hasta los diez decimales distintos. Todos estaban esperando que, a partir de un momento dado, los decimales se repitieran, que π fuera un decimal periódico. Si hubiera sido así, con ello habrían acabado el trabajo.
Poco después en 1615 el alemán Ludolf van Ceulen utilizó una fórmula parecida con treinta y cinco decimales. ¡Era una precisión tan enorme que durante un tiempo a π se le conoció como el número ludolfiano! El hombre estaba tan satisfecho con su descubrimiento que ordenó que a su muerte grabasen esos números en la lápida de su tumba, cosa que se hizo.
Fórmulas para hallar π, en 1673
A partir de cierto momento se puso de moda buscar fórmulas para calcular π de maneras cada vez más sencillas, aunque eso supusiera hacer larguísimos cálculos.Así, en 1673, un tal Wallis encontró una fórmula elegante:
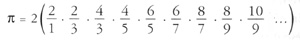
Leibniz otra:
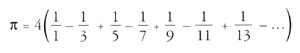
Estas fórmulas eran fáciles de entender, pero aproximarse a π requería miles de cálculos durante miles y miles de horas robadas al sueño o a otras diversiones. Aunque los matemáticos no se rendían, soñando que en algún punto aparecerían decimales periódicos. En 1706, el inglés Machin calculó cien decimales. En 1717, el inglés Sharp calculó setenta y dos…
Y el sueño se deshizo en 1761, cuando Lambert demostró que π era irracional. Eso significaba que nunca se encontraría ninguna fracción que diera un valor exacto y, además, que jamás se encontraría una periodicidad en sus cifras decimales.
Los matemáticos a veces son poco prácticos. Con los treinta y cinco decimales de Van Ceulen había más que suficiente para cualquier cálculo. Por ejemplo, si conociéramos el diámetro exacto del sistema solar (que nunca lo conoceremos, porque es variable) y quisiéramos calcular la longitud de la circunferencia que lo rodea (que ni existe ni serviría para nada el dato), los treinta y cinco decimales de Van Ceulen darían una precisión millones de veces más pequeña que un átomo.
Lo que quieren los matemáticos es conocer. Además, el dichoso π iba apareciendo en lugares cada vez más insospechados y no estaban dispuestos a que el número se les escapase de las manos. Utilizando fórmulas cada vez más complicadas, en 1844, Johann Dase llegó a 205 cifras decimales. Y, por último, en 1874, el inglés William Shanks calculó π con 707 decimales. En ese trabajo estuvo empeñado durante veinte años. Fue un descubrimiento tan importante que esos números fueron grabados en el Palacio de los Descubrimientos de París, en una gran sala … Circular, claro.
Nuevos descubrimientos, en 1882
El logro de Shanks fue el último de una época, porque en 1882 el alemán Lindemann demostró que π era trascendente. Es decir, que no podría ser solución de ninguna ecuación polinómica de coeficientes enteros. Traducido al lenguaje de la calle, eso significaba que, por mucho que se buscara, nunca se podría plantear ninguna ecuación que diese el valor de π. Para calculado, no quedaba más que la fuerza bruta, como la de Van Ceulen, la de Sharp o la de Shanks … Y nadie estaba por la tarea de dedicar más de veinte años de su vida a calcular unas cifras que no tenían ninguna utilidad práctica.
El famoso número durmió durante sesenta años. Nadie calculó más cifras; las de Shanks se consideraron buenas y aparecieron en muchos libros de matemáticas. Lo que sí se hizo fue buscar más fórmulas para calcular el valor de 1t con menos pasos y mayor eficacia. Por ejemplo, en 1914, el matemático indio Srinivasa Ramanuján creó una fórmula en la que a cada paso aparecían ocho decimales más. Cuando en la década de 1940 se inventaron los primeros ordenadores, los matemáticos dijeron algo así como: «Estas máquinas son rápidas, no necesitan descansar ni beber agua; pueden trabajar día y noche y no protestan… ¡Pues que calculen ellas!».
Esto ocurrió en 1949. Un año antes, un tal Ferguson había calculado 1t con 808 decimales, utilizando una calculadora mecánica, y ya había notado que había algunas diferencias con el valor obtenido por Shanks. En 1949, recién inventados los ordenadores, pusieron una máquina a machacar números durante setenta horas.
Hoy estamos tan acostumbrados a manejar ordenadores, consolas e internet que no imaginamos lo que era el trabajo de un «dinosaurio» informático como ENIAC, que era como se llamaba la máquina en cuestión. No tenía pantalla ni teclado.Ocupaba varias habitaciones llenas de paneles y amasijos de cables, con válvulas que se calentaban y estropeaban de vez en cuando. La máquina zumbaba y los técnicos la vigilaban, para que algunos componentes no se calentasen en exceso… Y al cabo de esas setenta horas escupió su cálculo: π ¡con dos mil treinta y cinco cifras decimales! Parecía una burla de Shanks y de sus veinte años de trabajo, porque además demostró que el pobre humano se había equivocado a partir de la cifra quinientos veintisiete.
Desde entonces, del «sucio trabajo» de calcular el valor de π se han ocupado los ordenadores. En 1957, se obtuvieron siete mil ochocientos decimales en treinta horas de cálculo. En 1961, cien mil cifras en ocho horas de cálculo. En 1967, medio millón de cifras en nueve horas de trabajo. En 1987, ciento treinta millones de cifras decimales. En 1994, cuatro mil millones. En 1997, el récord estaba en sesenta mil millones, pero en 2003 la cantidad ha crecido hasta algo más del billón… ¿Dónde estará cuando leas este libro?
Hoy en día, cualquier ordenador casero es capaz de calcular π con una precisión de mil decimales en unos pocos segundos, con tal de tener los programas adecuados. En cuanto a los ordenadores grandes, los matemáticos tratan de calcular cada vez más valores de π con tres propósitos. Uno, verificar si la máquina funciona bien; algo así como la prueba de «diga treinta y tres» cuando se va al médico. El segundo es comprobar nuevas fórmulas para generar π, fórmulas que a veces abren nuevos campos en el mundo de las matemáticas. El tercero es obtener cifras de π para estudiar algunas regularidades numéricas (no periodicidades, que son imposibles) que pueden resultar interesantes de cara a otros estudios.
Es casi seguro que π es el número más famoso de la historia, el que más tiempo de investigación ha requerido y el que ha hecho gastar más papel y horas de estudio en su cálculo o escritura. Sobre él hay miles de páginas en internet, en todos los idiomas. Para acabar este artículo, a partir de aquí van algunas ideas que pueden servir para añadir horas de estudio a la lista.
Tres
Si el número π tiene infinitas cifras decimales, se supone que dentro de él aparecerán, tarde o temprano, todos los demás números: el año en que naciste, las sumas de los cuadrados de las edades de tus padres, tu número de teléfono…En www.angio.net/pi/piquery. por ejemplo, se dice que el número del documento nacional de identidad del autor de este libro está en la posición 341.603a.
Catorce
La escritora polaca Wislawa Szymborska, premio Nobel en 1996, es una de las poetisas contemporáneas más originales. Escribió un poema titulado El Número Pi, que empieza así:
El número Pi es digno de admiración
tres coma uno cuatro uno
todas sus cifras siguientes también son iniciales
cinco nueve dos, porque nunca se termina…
Es casi seguro que solo sabiendo esto podrías localizar el poema completo con algún buscador de internet.
Quince
Existe un procedimiento curioso de calcular el valor de π con ayuda de un dardo, aunque requiere paciencia.

El asunto consiste en dibujar en una cartulina un cuadrado y su circunferencia inscrita y en disparar el dardo al azar, contando cuántas veces cae dentro del círculo y cuántas en el espacio que hay entre el círculo y el cuadrado.
(Lo más difícil es disparar al azar, porque uno tenderá a poner el dardo dentro del círculo, así que una solución sería tener media docena de monos que lo disparasen, pero esta es otra historia… Lo que hacen los científicos es escribir un programa de ordenador que «dispare» sobre el dibujo).
La probabilidad de que el dardo caiga en un sitio o en otro tiene que ver con las áreas del cuadrado y del círculo. Como en esta interviene π, podemos aproximamos a su valor.
Quienes han hecho este programa con ayuda de un ordenador han generado un millón de tiradas y han obtenido un valor de π con un error de dos centésimas por ciento.
¿Te atreves a calcular cuál es la probabilidad de que el dardo caiga en uno o en otro sitio?
Noventa y dos
La búsqueda de π ha generado un buen número de hallazgos en la historia de las matemáticas. La frase «cuadrar el círculo» quiere decir «pretender lo imposible». Proviene de un problema muy antiguo, consistente en construir un cuadrado de área igual a la de un círculo dado, en el que se empeñaron sin éxito muchos matemáticos. El problema se demostró imposible cuando Lindemann demostró que π era trascendente.
Pero quizá uno de los asuntos más ridículos tuvo lugar en el siglo XIX en el estado de Indiana, Estados Unidos. Un profesor “demostró” que π era igual a cuatro. Este profesor habló con un senador y este, ni corto ni perezoso (o tal vez las dos cosas) redactó una ley en la que .se establecía que π valía cuatro, que fue aprobada por la Comisión de Educación del estado. Además, el profesor patentaba el descubrimiento y cedía todos los beneficios a su estado, por lo que los políticos locales se mostraron muy agradecidos al profesor. ¡Increíble, pero cierto! El asunto no llegó al Congreso de EEUU porque un matemático aclaró las cosas e impidió un ridículo internacional.
Sesenta y cinco
π=3,141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521…